Preamble
A typical way of introducing complex numbers is as below:
Z = (a + ib)
where ‘Z’ is a “complex” number and i = √(-1) is the “imaginary” number. In addition, ‘a’ is called the “real part” and ‘ib’ is called the “imaginary part”.
The terms “real”, “imaginary” and “complex” do not convey the underlying concepts and lead to eternal confusion. Novice students are at a loss, and succumb to rote learning to get through exams. The basic concepts remain a mystery.
This blog provides an alternative way to introduce complex numbers and the concepts involved. It concludes by demonstrating that complex numbers are the most general form of a number!
Set of Positive Numbers
Human beings started using numbers to count physical objects, such as 5 apples, 6 oranges, etc. How the decimal system with symbols 0 to 9 came into popular use is a topic for another day.
Let us first consider the set of positive numbers including fractions (such as 3/2, 1/4, etc.), irrational numbers (such as √12, √5, etc.) and transcendental numbers (such as π = 3.14159…, e = 2.71828…, etc.). The set of positive numbers can be more conveniently represented in a graphical form as shown in Figure 1.
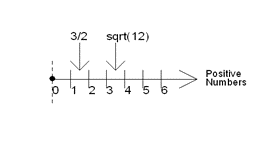Figure 1. Set of Positive Numbers
A set is said to be ‘closed’ for a given arithmetic operation, provided the resulting number of the operation is also in the set. Hence, a set of positive numbers is closed for addition, multiplication, division, and the square root. You can check this in a few examples, such as 3+5 = 8, 6×8 = 48, 3/2 = 1.5, sqrt(2) = 1.414… etc.
However, the ‘set of positive numbers’ is not necessarily closed for subtraction. For example, the set is closed for 5-2 = 3, but the set is ‘not closed’ for 2-5 = -3, since negative numbers are not a part of this set. Hence, we need to expand the set to include negative numbers to make our set closed for a subtraction operation.
Concept of Negative Numbers
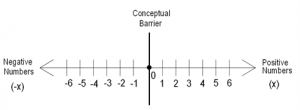
As we are already familiar with negative numbers, it appears to be a simple matter to extend our set to include negative numbers. This makes the set ‘closed’ for subtraction operations. Such a set is called a ‘Set of Real Numbers’! The set of real numbers can be illustrated graphically as shown in Figure 2.
Figure 2. Set of Real Numbers
The concept of negative numbers is not easy to comprehend. For example, what does ‘negative 5 apples’ mean? The negative number does not exist in the real world. We must pass a conceptual barrier shown in Figure 2 to visualise negative numbers. If we consider a conceptual barrier to be a physical wall, then negative numbers are literally behind the wall and can only be imagined. We cannot go there physically! It is not easy to penetrate this mental barrier. Apparently, Greek philosophers were aware of negative numbers, but they were not comfortable with them! In fact, the term ‘Negative’ has an implication of ‘False’ or ‘Not True’ or ‘Non-Existing’. This terminology did not help its conceptualisation. Romans went a step further and eliminated ‘Zero’ (Nothing) and Negative (False) numbers from their number system. For them, they were impractical and fictitious numbers.
Thanks to the Romans, the western world had to wait until 1202AD for the introduction of the decimal system by Fibonacci (Italian Mathematician) in his book Liber Abaci – Modus Indorum (Book of Calculation – Method of Indians). Negative numbers were first documented by Cardano (Italian Mathematician) in his book Ars Magna (Great Art) in 1545 AD. Even Leibniz (Father of Calculus 1646-1716AD) maintained that negative numbers were invalid but still used them in intermediate calculations. The result had to be positive – always!
Ironically, Brahmagupta (Indian Mathematician) wrote a book in 628AD, which included a detailed treatise on zero, negative numbers, square roots, and quadratic equations. He had no problem with the conceptualisation of negative numbers, since he used the terminology ‘Fortune’ for positive numbers and ‘Debt’ for negative numbers. This shows how a simple change of terminology can eliminate mental barriers!
Once we accept the negative numbers conceptually, a whole new dimension (world) opens. We can then find a multitude of practical uses for negative numbers. Hence, our generation has no problem accepting negative numbers, since we have an understanding of the practical uses of them.
Square Root of a Negative Number
A set of Real numbers (Figure 2) is a closed set is closed for addition, subtraction, multiplication, and division. However, the set of Real numbers is not necessarily ‘closed’ for the ‘square root’ of a number, since a negative number is now a part of the set. For example, -2 is a part of the set, but √(-2) is not a part of the set, as it is not possible to locate √(-2) on Figure 2.
The square root of a negative number was encountered by Cardano while solving cubic equations. He was trying to solve the following cubic equation.
x3 = 15x + 4
A cubic equation has at least one real root. Cardano’s equation was designed to provide the value of the real root. However, using his equation, Cardano ended up with the following result.
x = 3√(2 + √-121) + 3√(2 – √-121)
By trial and error, his colleague Bombelli knew that the answer was 4, so he went about a way to prove it. He wrote the above equation in the following form.
3√(2 + √-121) = a + bi
3√(2 – √-121) = a – bi where ‘i’ = √-1
After some algebraic manipulation, he found that a = 2 and b = 1. Hence the value of the real root is as given below.
x = (a + bi) + (a – bi)) = (2 + 1i) + (2 -1i) = 4
By the above methodology, Cardano and Bombelli had formalised not only the so-called ‘Imaginary Number’ but also ‘Complex Numbers’. However, their interest was only in the solution of cubic equations and did not continue the work further.
Coming back to the topic, we are interested in a set which is closed for the square root of a negative number. This can be achieved by including √-1 as a part of the set. However, looking at Figure 2, we realise that it is not possible to locate √-1 as a part of the line representing the ‘Set of Real Numbers’.
Rene Descartes (1596 – 1650 AD), also known as the Father of Geometry, cynically coined the term “Imaginary Number” for √-1, since he could not represent it geometrically, since he was using Figure 2. In addition, the term ‘Complex Number’ has only added to the mystery and confusion. We are now stuck with these terminologies and eternal confusion. The aim of this blog is to clear this confusion and present the concept in a logical way.
Euler’s Equation and Complex Numbers
Leonhard Euler (1707 – 1783 AD) was a Swiss mathematician, who spent most of his adult life in Russia and Germany. He is one of the greatest mathematicians of all time. It is Euler who formalised the symbols for transcendental numbers ‘e’ and ‘i’, namely, Exponential constant (e = 2.718…) and for the Imaginary number (i = √-1). He also developed a relationship between ‘e’ and ‘i’ which paved the way for representing imaginary numbers geometrically! The famous equation which related these transcendental numbers is called the Euler’s equation, which is given below.
eiθ = cos(θ) + i sin(θ) … (1)
where θ is an angle in radians or degrees with respect to a reference.
Euler’s equation effectively defines a ‘Complex’ number. This definition dramatically changed the perception and the use of ‘Complex’ numbers. Let us examine how the Euler’s equation helps us to visualize and geometrically plot complex numbers.
Let us consider a number from the set of Real numbers, for example: 5. This ‘real’ number can be expressed as a ‘complex’ number using Euler’s equation by setting the value θ as 0 radians or degrees.
5ei0 = 5 (cos(0) + i sin(0) )
= 5 (1 + i0) = (5 + i0) = 5
Hence, the Euler’s equation results in a positive real number ‘5’ for our example. This value can be plotted in a traditional way on the horizontal axis as shown in Figure 3. In other words, the value is on the ‘x’ axis or the ‘Real’ axis!
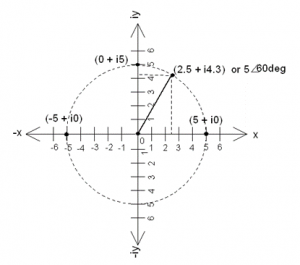Figure 3. Geometric Representation of Complex Numbers
Let us set θ = π radians (180 degrees) and see what happens.
5ei π = 5 (cos(π) + i sin(π) )
= 5 (-1 + i0) = (-5 +i0) = -5
The Euler’s equation now results in a negative (real) number. This number can again be plotted as shown in Figure 3.
Let us set θ = π/2 radians (90 degrees) and see what happens.
5ei π/2 = 5 (cos(π/2) + i sin(π/2) )
= 5 (0 + i1) = (0 + i5) = i5
Note that i5 = √(-1) x 5 = √(-1) x √(25) = √(-25)
For this example, the Euler’s equation results in the square root of a negative number or the so-called ‘Imaginary’ number. But we can locate this value geometrically as shown in Figure 3. The number ‘i5’ is on the ‘y’ axis, since the angle θ is set at 90º with respect to our reference axis, namely the ‘x’ axis. An inspection of Figure 3 reveals that the ‘imaginary’ number (i5) is essentially the same number 5 rotated by π/2 radians 0r 90 degrees.
Lastly, let us set θ = π/3 radians (60 degrees) and see what happens.
5ei π/3 = 5 (cos(π/3) + i sin(π/3) )
= 5 (0.5 + i0.866) = (2.5 + i4.33)
We can plot this value geometrically as shown in Figure 3. A closer inspection of Figure 3 reveals that 5ei π/3 is essentially the number 5 rotated by π/3 radians 0r 60 degrees. Another form of representing this number is (2.5 + i4.33), which is the projection of number ‘5’ on the ‘x’ and ‘y’ axis. The diagonal distance of the point from the origin (reference point) represents the number ‘5’.
If we repeat the above process for various values of θ, then we can see that number 5 moves along the dotted line (circle) shown in Figure 3. In other words, we can use the ‘complex number’ to represent the position of a point in two dimensions. It is no longer an ‘imaginary’ or ‘complex’ number, but it is a number in a two-dimensional space. Hence, it is useful in practice to locate the position of objects in two dimensions.
The traditional number system is a one-dimensional number system, as they can only represent the values in one dimension (Refer to Figure 2). However, as per Figure 3, we now have a number in two dimensions. Hence, we can say that the ‘complex’ number is a more general form of a number. The ‘Real’ number, which we use in our daily transactions, is a particular case (Real part) of a complex number!
Complex Number – Cartesian and Polar Form
There are two popular ways of representing complex numbers in practice. They are called the ‘Cartesian’ form and the ‘Polar’ form. The term Cartesian is derived from the name Rene Descartes, the famous French mathematician previously mentioned. He developed methods for plotting algebraic functions as geometrical shapes using two dimensional plots. In other words, the familiar x-y plots.
Cartesian Form
The Cartesian form is the right-hand side of the Euler’s equation (Equation 1). Let us refer to the left-hand side of the equation as the ‘Exponential’ or the ‘Euler’s’ form. Both forms are used to represent the same value. For example:
5ei60º = 5 (cos(60º) + i sin(60º) ) = (2.5 + i4.33)
The right-hand side value, namely (2.5 + i4.33), is called the Cartesian form. This form is simpler for complex number addition and subtraction. The Cartesian form can also be used for multiplication and division, even though it is more cumbersome.
The exponential form is simpler for multiplication and division, but performing addition and subtraction is not feasible without converting to the Cartesian form.
This is illustrated below using complex numbers A and B. In printed documents, a bold font is usually used to represent complex variables.
A = 5ei60º = (2.5 + i4.33)
B = 4ei30º = (3.464 + i2)
Multiplication using Exponential form:
A x B = 5ei60º 4ei30º = 20ei(60º+30º) = 20ei90º = (0 + i20)
Multiplication using Cartesian form:
A x B = (2.5 + i4.33) x (3.464 + i2)
= (2.5 x 3.464 + 2.5 x i2 + i4.33 x 3.464 + i4.33 x i2)
= (0 + i19.999) [ Use i2 = -1 for simplification]
= 19.999 ei90º [ Note the error due to rounding ]
Hence, multiplication (and also division) is simpler in the exponential form.
Now, let us try addition using the Cartesian form:
A + B = (2.5 + i4.33) + (3.464 + i2)
= (5.964 +i6.33)
= √(5.9642 + 6.332) ei tan-1(6.33/5.964)
= 8.697 ei46.71º
Addition using Exponential form:
A + B = 5ei60º + 4ei30º = ???
There is no straightforward way of doing the above addition. Normally, the A and B are converted to Cartesian form and the addition is performed! The result is then converted back to exponential form!!
With modern calculators and computers, the above discussion is irrelevant since these machines can handle complex numbers directly. The input values are normally entered in Cartesian form, and the results are also in Cartesian form. The values can be converted into exponential form, if required.
Polar Form
The polar form is used extensively as an alternative to Euler’s (exponential) form. The polar form arbitrarily ignores the presence of the exponential (‘e’) and imaginary number (‘i’). An example of the polar form of a complex number is as shown below.
A = 5ei60º = 5 ∟60º
5 ∟60º is called the Polar form. There is no mathematical basis for this simplified form. The polar form looks simpler and elegant, but it hides important information. However, its usage is so ubiquitous in practice to represent complex numbers that most people forget the original Euler’s equation from which it was derived. It has done a great disservice to the concepts in complex numbers. Hence, we should always visualise the Euler’s form whenever we see or use the polar form.
Complex Numbers are a ‘Closed Set’
We started this blog in search of a set of numbers which are ‘closed’ for all mathematical operations. Just to recap, the term ‘closed’ specifies that the result of a mathematical operation on numbers in the set must also be a part of the set.
The problem of negative numbers due subtraction operation was solved by including the negative numbers as a part of the set. Even though it may look trivial, it took almost 300 years to accept negative numbers in the western world, after the introduction of decimal numbers in 1202 AD.
Similarly, when the problem of the ‘square root of a negative number’ was encountered, it could have been easily solved by accepting √(-1) as a part of the number system. We could have defined this ‘generalised number’ as a two-part number. For example:
(3 + √-4) = (3 + √-1 √4 ) = (3 + i2) where i = √-1
This simple concept became too confusing by the unnecessary introduction of the terms ‘imaginary’ and ‘complex’ numbers. It is essential to transcend these terminologies to truly understand and appreciate complex numbers!
The famous mathematician and physicist Carl Friedrich Gauss(1777-1855), who has contributed extensively to complex algebra, made the following statement, in his thesis Gauß, Werke, Bd. 2, S. 178.
“If this subject has hitherto been considered from the wrong viewpoint and thus enveloped in mystery and surrounded by darkness, it is largely an unsuitable terminology which should be blamed. Had +1, -1 and √−1, instead of being called positive, negative and imaginary (or worse still, impossible) unity, been given the names say, direct, inverse and lateral unity, there would hardly have been any scope for such obscurity.”
Coming back to where we started, we can now verify that the set of complex numbers is a closed set! In other words, any arithmetic operation on complex numbers results in a complex number. Let us consider the worst case, the square root of a negative complex number is a complex number! Let us examine it.
Example:
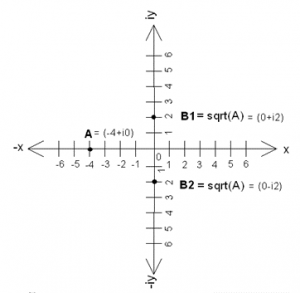
Calculate the square root of the complex number A = (-4 +i0).
Even though we have used -4 (a negative real number!) as an example, the following procedure is applicable to any complex number.
Let’s first express the complex number in exponential form.
A = (-4 + i0) = -4 (1 + i0) = -4 ( cos(0) + i sin(0) ) = -4 ei0º
To avoid taking the square root of a negative magnitude (number), we can replace the negative sign by adding 180º to the angle. This does not alter the value of A.
A = 4 ei(0º +180º) = 4 ( cos(180º) + i sin(180º) ) = (-4 +i0)
Let B1 be equal to the square root of A.
B1 = √(A) = √( 4 ei180º ) = ( 4 ei180º )1/2 = 41/2 ( ei180º )1/2 = 2 ei180º/2
= 2 ei90º = 2 (cos(90º) + i sin (90º) ) = (0 + i2)
Voila! The square root of a complex number is a complex number. Hence, the set of complex numbers is a closed set.
We can check the result. B1 x B1 = (i2) x (i2) = i2 4 = -4 (Remember that i2 = -1)
A positive number has two roots, namely √4 = +/- 2. Similarly, even negative and complex numbers have two roots! In fact, the second root is the negative of the root value calculated above. Let us say, the second root is B2.
B2 = –B1 = – (0 + i2) = (0 – i2) = 2 e-i90º
Again, we can check the result. B2 x B2 = (-i2) x (-i2) = i2 4 = -4
Note: We could have also obtained the second root B2 directly by using 4 ei(0-180º) instead of using 4 ei(0+180º) to represent -4 ei0º for the square root calculations.
The above values can be plotted on a two-dimensional plane as shown in Figure 4.
Figure 4. Square root of a Complex Number
In general, the square root of a complex number can be obtained as below.
Given A = Aeiθ , the square root is B = √(A) = (√A) eiθ/2. In other words, it is the ‘square root’ of the Magnitude and the Angle is halved. The second root is the negative of the calculated root.
Practical Relevance of Complex Numbers
Referring to Figure 3, we can observe that a complex number is a two-dimensional number! Hence, it can be used to locate any point on a two-dimensional space.
Complex numbers can be used to represent physical quantities with two components. Hence, they can be used to represent physical quantities such as Force, Velocity, etc which have a magnitude and a direction. The direction can be represented as an angle to the reference axis.
The most common practical application of complex numbers is to represent sinusoidally varying voltage and currents in Alternating Current (AC) electrical systems. Incidentally, AC voltages and currents can be represented by magnitudes (real numbers) only, provided there is no ‘phase difference’ between the quantities. This happens only in the case of resistive circuits. Practical AC systems are always associated with alternating magnetic and electrostatic fields. This introduces the ‘phase difference’ between AC voltages and currents. In general, AC quantities have a magnitude and a phase angle with respect to a reference quantity. Hence, complex numbers are an essential part of AC systems analysis.
There is another interesting scenario, which occurred in quantum mechanics. When Erwin Schrodinger (Austrian, 1887-1961) developed the famous ‘Wave’ equation, he was surprised to find the ‘Imaginary’ number (i) in the equation. He and other physicists were not comfortable with it, since they felt that the quantum particle exists in the real world and it is not ‘Imaginary’! Efforts were made to develop the Schrodinger’s wave equation using only real variables. However, when actual experiments were conducted for particle motion, it was found that only the predictions made with ‘complex variable’ equations matched the experimental results! A link to a detailed blog on this topic is available in the Reference section. The blog also gives the colourful history of imaginary numbers.
Conclusions
The main aim of this blog was to introduce complex numbers as the most general form of numbers, since the set of complex numbers is a closed set for all arithmetic operations, including the square root of a negative number!
Rene Descartes was responsible for coining the term ‘Imaginary’ number for the square root of a negative number. He did so because he could not represent the square root of a negative number geometrically (Refer to Figure 2). We have now solved Descartes’s problem (Refer to Figure 4). Thanks to Descartes, subsequent generations were destined to live with the confusion caused by the term ‘Imaginary’ number. Hopefully, this blog has solved the conceptual problem for future generations!
The credit for making complex numbers useful goes to Euler, who conceived the Euler’s equation. It is one of the most famous equations, comparable to that of Albert Einstein’s equation (E = mc2).
I will conclude this blog by presenting the most beautiful equation in mathematics, which is derived from the Euler’s equation:
eiπ + 1 = 0
You can derive the above equation by setting θ = π in the Euler’s equation. Try it out!
The above equation has three important transcendental numbers (e, π and i) along with existence (1) and non-existence (0). It may hold the secrets to the universe!
Reference
https://www.scientificamerican.com/article/quantum-physics-falls-apart-without-imaginary-numbers/
