AC meters and ‘rms’ values
The simplicity and extensive use of Equation 9 for AC power calculation comes at a conceptual cost. This is further compounded by the fact that AC meters are designed to measure and display ‘rms’ values directly. This gives an impression that ‘rms’ values are physical quantities. This is not true. The physical quantity is the ‘peak’ or the ‘maximum’ value of the sinusoidal variation. The ‘rms’ value is a fictitious mathematical quantity, which was introduced for the convenience of calculating the ‘average power’ in AC systems!
With the use of Equation 9 for AC power calculation, a novice electrical engineer tends to forget that they are dealing with time varying sinusoidal quantities. Also, Equation 9 is only valid for the specified conditions, namely for unity power factor or resistive loads. Let us explore this through the following examples.
Example 2
A hot water kettle is supplied from a 240 V mains power outlet. The voltmeter (V) connected across the mains reads 235 V and the ammeter (A) connected to the kettle reads 5 A. Calculate the average power over one cycle assuming sinusoidal steady state conditions.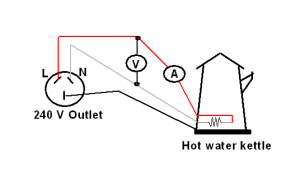
The values displayed by the AC meters are ‘rms’ values. Hence, we can use Equation 9 for average power calculation.
Pav = P = E I = 235 V x 5 A = 1,175 W or 1.175 kW
Note: 240 V is the rated nominal voltage of the power outlet. The actual voltage depends on the network conditions. However, the power systems are designed to ensure that the actual voltage is with the limits specified in the standards.
Example 3
A pump motor is supplied by a 240 V mains power outlet. The voltmeter (V) connected across the mains reads 235 V and the ammeter (A) connected to the motor reads 5 A. Calculate the average power over one cycle assuming sinusoidal steady state conditions.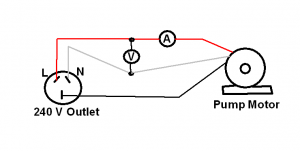
Using Equation 9, we can calculate the average power as given below.
Pav = P = E I = 235 V x 5 A = 1.175 kW (???)
Is the calculated value of ‘Average power’ correct?
What is the required condition for using Equation 9? Does the pump motor meet that condition?
Epilogue
Examples 2 and 3 illustrate the serious conceptual problem when using Equation 9 for AC systems. The results are valid for Example 2, as the hot water kettle is a resistive or unity power factor load. The results are not valid for Example 3, as motor load is not a resistive or unity power factor load.
The concepts and derivation of a generalised equation for AC power calculations will be discussed in the next blog! This blog will also clearly present the concept of ‘Reactive power’ and ‘Power factor’!
