Three_phase_systems_pt_1_why_three_phase

Power in Two Phase Systems

Let us now investigate the power flow in a two phase system.  A simple schematic for a two phase system is as shown in Figure 2.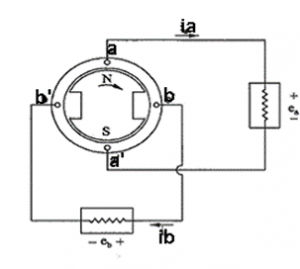Figure 2 – Two phase system schematic

A two phase system consists of a generator with two independent coils a-a’ and b-b’, which correspond to the two phases.  The coils are identical, but the two coils are located at 90 electrical degrees from each other.  For a two pole machine, 1 electrical degree is equal to 1 mechanical degree.  Due to the physical location of the coils, the voltage induced in coil b-b’ lags the voltage induced in coil a-a’ by 90 electrical degrees.

The two coils are connected to their own independent load as shown in Figure 2.  Let us assume that the two loads are identical.  In other words, we have a ‘balanced’ system.  We can now write the following equations for voltage, current and power as below.

For the coil a-a’ or phase ‘a’ system:

e_a  =  E_m cos(ωt)

i_a   =  I_m cos(ωt)

p_a  =  e_a i_a  =  E_m Im cos²(ωt)

For the coil b-b’ or phase ‘b’ system:

e_b  = E_m cos(ωt-90º)  =  E_m sin(ωt)

i_b   = I_m cos(ωt-90º)   =  I_m sin(ωt)

p_b  =  e_b i_b  =  E_m I_m sin²(ωt)

Note that the coil ‘b’ voltage lags the coil ‘a’ voltage by 90º (electrical).

The total electrical power generated by the machine at any given instant of time is:

p_total  =  p_a + p_b

                                                =  E_m I_m cos²(ωt) + E_m I_m sin²(ωt)

We have cos²(ωt) + sin²(ωt) = 1, hence we can write:

p_total  =  E_m I_m                             …(1)

The result obtained in Equation 1 is interesting!  It shows that the ‘total power’ generated by the machine at any given instant of time is constant!!  To reinforce this concept, the powers p_a, p_b and p_total are plotted and is as shown in Figure 3.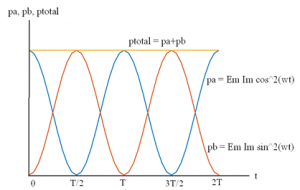

Figure 3 – Waveforms for power in a two phase system

We can now write the total electric power in a two phase system as below:

P_2ph  =  p_total   =  E_m I_m   =  2 (E_m/√2) (E_m/√2)

=  2 E_rms I_rms    watts          … (2)

It can be observed from Equation 2 that the total power in a two phase system is two times the average power of a single phase system.  More importantly, the total electrical power output is constant with respect to time.  Note that upper case P has been used for ‘P2ph’, since the ‘total power’ is constant with respect to time.

Advantages of a two phase system

The ‘total’ power output of a two phase system is constant with respect to time.  Hence, the mechanical power input to the prime mover will be constant with respect to time.  This feature eliminates the need for a flywheel and provides for an economical and robust mechanical design of the generating system.

As per the schematic in Figure 2, a two phase generator can produce twice the power of the single phase generator.  In practice, a two phase generator will be smaller and more economical than a single phase generator for a given power level.